Entropy, Redundancy and Inequality Measures

Atkinson
inequality

Z_Atkinson = 1-Z_MacRae^[1] ≥ 1-exp(Σ_i=1..N(E_i*ln(A_i/E_i))/E_total)*E_total/A_total

nosniktA
inequality

Z_nosniktA ≥ 1-exp(Σ_i=1..N(A_i*ln(E_i/A_i))/A_total)*A_total/E_total

Theil-T
redundancy

R_Theil	= -ln(1-Z_Atkinson) = -ln(Z_MacRae)
	≥ ln(A_total/E_total) - Σ_i=1..N(E_i*ln(A_i/E_i))/E_total

Theil-L
redundancy

R_liehT	= -ln(1-Z_nosniktA)
	≥ ln(E_total/A_total) - Σ_i=1..N(A_i*ln(E_i/A_i))/A_total

Theil-S
redundancy

Symmetric
redundancy


R_sym	= -ln(1-Z_sym) = 2Z_Platoartanh(Z_Plato)
	= (R_Theil(E\|A)+R_Theil(A\|E))/2 = (R_Theil+R_liehT)/2
	≥ Σ_i=1..N(ln(E_i/A_i)*(E_i/E_total-A_i/A_total))/2

Symmetric
inequality

Z_sym	= 1-exp(-R_sym) = 1-√((1-Z_Atkinson)*(1-Z_nosniktA))
	≥ 1-exp(Σ_i=1..N(ln(A_i/E_i)*(E_i/E_total-A_i/A_total))/2)

Hoover
inequality

Z_Hoover ≥ Σ_i=1..N|E_i/E_total-A_i/A_total|/2

Coulter
inequality

Z_Coulter ≥ √(Σ_i=1..N(E_i/E_total-A_i/A_total)²/2)

Gini
inequality

sort data: E_i/A_i>E_i-1/A_i-1
Z_Gini ≥ 1-Σ_i=1..N((2*Σ_k=1..i(E_k)-E_i)*A_i)/(E_total*A_total)

EU
inequality

1:a = (1-Z_Gini)/(1+Z_Gini) is the SOEP "equality parameter"
therefore: Z_Europe = 2*Z_Gini/(1+Z_Gini)

Plato
inequality

inverse functions:
   Z_sym = 1-((1-Z_Plato)/(1+Z_Plato))^Z_Plato
   R_sym = 2*Z_Plato*artanh(Z_Plato)
approximation:
   Z_Plato ≈ 1 - arcsin((1-Z_sym)^{(0.06*Z_sym+0.61)})*2/π, error < 0.002 for Z_sym < 0.75
fast recursion (there is a better version in onOEI-1.0.5.py):
   initialize: Z_Plato ≈ 1 - arcsin(exp(R_sym(0.06/exp(R_sym)-0.67)))*2/π
   repeat:
      Z_last = Z_Plato
      Z_Plato = tanh(R_sym/(Z_Plato+Z_last))
      until 2*Z_Plato*artanh(Z_Plato) - R_sym is small enough.
format for comparison to the "Pareto Principle":
   a : b = (1+Z_Plato)/2 : (1-Z_Plato)/2
   Z_Plato = |2a-1| = |2b-1|

Redistributive
Aggression

R_A	= (R_Theil+R_liehT)/2 - Z_Hoover = R_sym - Z_Hoover
	= Σ_i=1..N(ln(E_i/A_i)*(E_i/E_total-A_i/A_total) - \|E_i/E_total-A_i/A_total\|)/2

Any city however small, is divided at least into two,
one the city of the poor, the other of the rich;
these are hostile to each other.
(Plato, Politeia, 370 BC)

Blog (closed): blog.umverteilung.de since 2009-08-25, so far mostly in German. Errata and updates for poorcity.richcity.org will be posted in blog.umverteilung.de/en.
Internal Links and Downloads: Spreadsheet for Theil index computations | Printed Spreadsheet (PDF) | Spreadsheet Update (2021, f. Libre Office) | Inequality issuization (PDF)
External Links (Germany): BMAS (2008-09): Einkommens- und Vermögensverteilung | wemgehoertdiewelt.de | sozialpolitik-aktuell.de
Tools: Calculator (in English) | Rechner (in Deutsch)
New tools (November 2008): Python scripts (Formulas in Amartya Sen's On Economic Inequality and my own algorithms) | Einkommen 2004 (Income 2004) | Einkommensanalyse für Unternehmen und Betriebsräte (Income analysis for enterprises and works councils)

U.S. Census Bureau, 2007: Income Distribution to $250,000 or More for Households (Table HINC-06) and inequality measures
A bit off topic (April 2009): Economic Growth | Information and e | From Discrete to Continuous

Example:
Wealth Distribution,
Germany 1995

A	E

50%	2.5%
40%	47.5%
9%	27.0%
1%	23.0%

Source: SPD, German Parlament,
Bundestagsdrucksache 13/7828

Computation:
Engl., Ger.

N=4

Z_Atkinson ≥ 64.1%
Z_sym ≥ 68.7%
Z_Hoover ≥ 47.5%
Z_Gini ≥ 64.5%
Z_Plato ≥ 64.8%

Variables:
- A_i: "people" (amount of individuals in group_i of a society), A_total=Σ_i=1..N(A_i)
- E_i: "wealth" (total wealth owned by that group_i of a society), E_total=Σ_i=1..N(E_i)
- N: amount of groups (quantiles, percentiles) in the society
- Z_...: inequality measure for society (unified group, all groups)
- R_...: redundancy (maximum entropy of society less actual entropy of society)
Remarks:
(1) This calculus follows the notation used in the calculus from Lionnel Maugis^[2] (1996).
(2) In this calculus N only is used as upper limit for the index of Σ.
(3) Usualy I use the %-format for normalized measures.
(4) The formulas for grouped data yield mimimum values because the inequalities within the quantiles are not evaluated. Higher granularity (division of a population into more quantiles) usualy also yields higher inequalities and higher redundancies.
Redundancy, Equality, Inequality:
Entropic inequality measures like Theil's entropy actually are not entropies. They are redundancies^[3]. The redundancy of a system at a given time is the difference between its maximum entropy (e.g. Theil: ln(A_total/E_total)) and its present entropy (e.g. Theil: Σ_i=1..N(E_i*ln(A_i/E_i))/E_total^[a]) at that time.
In a system a certain amount of transformations is possible. The sum of transformations, which already have occured, cannot be reversed without help from outside. Entropy is a measure for how many transformations already have occurred in that system. The redundancy serves as a measure for how many transformation opportunities still are available. If completely equal distribution (of whatsoever) in a system leads to maximum entropy of that system and if low entropy of that system is caused by high distributional inequality, then achieving equal distribution means that the distribution process is saturated. In that case a relative equality measure can be defined using the term e^-R, where R is the redundancy (the remaining distribution possibility) of the system and e is Euler's constant^[b]. As for the relative inequality, Z=1-e^-R applies.
In this text, "symmetric" does not stand for invariance under permutations of individuals. Rather, I define inequalitiy measures as being symmetric, if Z(E|A)=Z(A|E); and redundancies are symmetric, if R(E|A)=R(A|E). Gini's, Hoover's and Coulter's inequalities are symmetric. Theil's redundancy and Atkinson's inequality are not symmetric. Therefore the symmetric inequality Z_sym has been introduced: It simply is derived from the symmetric redundancy R_sym which is half of the sum of Theil's redundancy Z_Theil(E|A) and Theil's redundancy with swapped data Z_Theil(A|E) .
You may interpret redundancy as a measure for distributability of resources. (Whether redundancy is "good" or "bad" usualy depends on who benefits from it and who controls it - which usually is the same.) For living systems (individuals, societies) redundancy is the distance between life and death.

Plato Inequality:

This inequality measure is inspired by Plato: The Plato inequality refers to Plato's "two cities", a city devided into at least two quantiles. Example: A Plato inequality of 60% describes an inequality, which is similar to the Symmetric inequality of a society devided into two quantiles, where in one (bigger) quantile a share of 80%=(100%+60%)/2 of the citizens control only a share of 20%=(100%-60%)/2 of all resources, and in the other (smaller) quantile a share 20% of the citizens control a share of 80% of all resources. Examples:
median, Europe: 20.0% 25.0% 33.3% 40.0% 50.0% 57.1% 66.7% 75.0% 78.6% 80.0% 85.7% 88.9% Plato, Gini, Hoover: 11.1% 14.3% 20.0% 25.0% 33.3% 40.0% 50.0% 60.0% 64.8% 66.7% 75.0% 80.0% Z.sym: 2.5% 4.0% 7.8% 12.0% 20.6% 28.7% 42.3% 56.5% 63.2% 65.8% 76.8% 82.8% R.sym, Theil: .025 .042 .081 .128 .231 .339 .549 .832 1.000 1.073 1.459 1.758 Aggression: -.086 -.101 -.119 -.122 -.102 -.061 +.049 +.232 +.352 +.406 +.709 +.958 A1=E2: 4444 4285 4000 3750 3333 3000 2500 2000 1760 1667 1250 1000 E1=A2: 5556 5715 6000 6250 6667 7000 7500 8000 8240 8333 8750 9000 ^{"Pareto Principle"}
Applied to Plato's two-quantile-societies, the formulas for Plato's, Gini's and Hoover's inequality yield similar results. Also the formulas for the Symmetric redundancy and Theil's redundancy yield similar results. The Plato inequality behaves almost like the Gini inequality, as the blue "cluster" along the diagonal line in the graphics below (next paragraph) shows. But as an advantage over the Gini inequality, the Platon inequality can use the full range between 0% and 100% independently from the amount of quantiles.
The computation of the Plato inequality can be done by recursive iteration. The procedure is implemented in the on-line calculator attached to this site. The recursion quickly will yield a result with any precision you need.
In comparison to other inequality indicators, the Plato inequality (as well as its parent, the Symmetric inequality) also is one of the most sensitive indicators for indicating the existence of deprived minorities.

From Numbers to Meaning

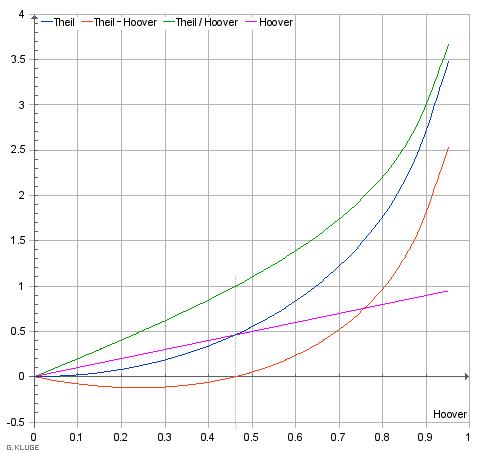
Relation between Theil Redundancy and Hoover Inequality for 2-quantile-societies.
(For such societies, the Gini Inequality is equal to the Hoover Inequality.)

"A [Gini] coefficient of 0.3 or less indicates substantial equality; 0.3 to 0.4 indicates acceptable normality; and 0.4 or higher is considered too large. 0.6 or higher is predictive of social unrest." Liu Binyan, Perry Link: A Great Leap Backward?, 1998-10-08

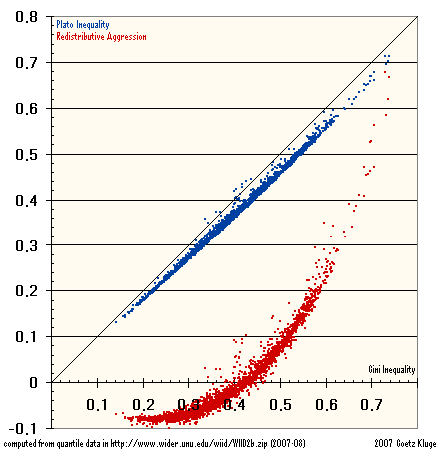
Statements like the one above suffer not only from the lack of explanation how the Gini inequality was computed. You also want to know the sources. One approach is to look at the WIID database and to check, which countries are known for social unrest and what inequality measurements you get from these countries. Then you probably will agree to Liu Binyan's and Perry Link's statement. And I think, that also a redistributional aggression measure (which I introduce in the next paragraph) matches with the realities found between Scandinavian welfare and Latin American redistributional violence in the countries of the WIID database.
It is widely accepted, that property is distributed with a Gini index of 60%. How do you feel about that statement? Do you feel better with the statement, that in many cases 80% of the people own 20% of property and 20% of the people own 80% of property? You cannot reject the first statement and accept the second statement at the same time, as for such two-quantile-societies both statements are the same simplifications. Nevertheless, the 80:20 "Pareto Principle" is more than just a truism due to its proximity to 82:18, where the Theil redundancy is 100%. It seems to mark a frequent distribution of property and asset usage. Also we know, that a Gini index of 60% is related to more violent modes of redistribution. That is why property needs protection by law, police and physical barriers. As for incomes, distributions with a Gini index around 45% and below are what you expect in civilized countries without too much need to call in the police in case of conflicts. Whereas in case of property distribution a Theil redundancy of 1 should be checked for being a valid marking point, in case of income distribution the point, where Theil's redundancy and Hoovers inequality are similar, could be an interesting mark. Check the difference between both as a measure vor redistributive aggression.
If you question the 80:20-"principle" and reject giving a Gini inequality around 45% some special normative meaning, then you still can look for norms discovered by empirical research: Yoram Amiel and Frank Cowell^[8] let students make judgements on sample inequalities. They "calibrate" inequality measurements empirically and also analyze, how the properties of inequality measures (anonymity, scale invariance, translation invariance, scale independence, translation independence, population principle, transfer principle and decomposability) are related to such judgements. This research gives sense to inequality measurement.
Outside of the lab, inequality rarely presents itself to the majority of people in quantiles or cake diagrams. Here empirical research could analyze, how happy people are with the distribution of ressources in their region. How important an issue is distributional justice? Should the government increase or decrease redistribution by taxation and other transfers? And if in a region there is something like a free press, you could analyze, how important inequality issues are to the media? This then could be correlated with measured inequalities and with the measured redistributive aggression (inequality issuization.)

Between Playfield and Battlefield:

Unfair distribution of wealth (wether factual or alledged) leads to fury (aggression). The market turns into a battlefield. On the other side people do unterstand, that guaranteeing the same income for everyone also means, that there must be some artificial control of income distribution which also deprives them from the chance to increase their income by increasing their contribution to society. Equalitarian control attempts to close the battelfield, but it also closes the playfield. Therefore the majority of people expect (negative aggression) a certain inequality of distribution but reject (positive aggression) inequalities which they consider to be extreme.

Plato Inequality and Redistributive Aggression (Inequality Issuization) over Gini Inequality (2007-08-18)

There is an inequality measure which takes care of the fact, that aggression against inequality can be positive and negative: The Redistributive Aggression is defined to be the difference between plain inequality weighted by perception (the Symmetric redundancy) and the unweighted plain inequality (the Hoover inequality). This aggression measure is a social entropy measure. Or you interpret it as a redundancy measure for those to whom redistribution is a business. And if "aggression" sounds too emotional, you also may call the measure Inequality Issuization.
The measure for Redistributive Aggression can take positive and negative values: Negative values indicate playful competition between gamers rather than between enemies. Positive values indicate a seriously aggressive competition. High positive values mark a high level of hostility. The measure can increase beyond +1. (You could normalize the measure by Z_A=1-e^-R_A in order to limit the positive side to +100%. The negative side practically will never go below -100%. By the way: For most real world income inequalities: R_A≈Z_A.)
For Plato's two-quantile-societies given above, a Gini inequality of 0% for incomes can be associated with a total standstill, but at 25% you feel like in Scandinavia and would tolerate even higher inequality without envy. Above an income inequality of 40%, people compete in the tougher British, German and American ways: Friendliness becomes "professional" and ritualized, the robot on the phone calls you a "valuable customer". In these societies people had to learn to give aggressiveness a positive connotation. But a society with a income inequality of above 60% usually will be known for corruption, crime and bloodshed. Once the income inequality would exeed 80% and/or the Redistributive Aggression would go beyond +1, probably plain terror would rule the relation between Plato's poor city and rich city.
The Redistributive Aggression measure offers a way to indicate a range of inequality, which people not only tolerate, but even may appreciate. The question is not about whether or not to tolerate inequality. It is about the degree of inequality. The playfield is marked by negative aggression, the battlefield is marked by high positive aggression measures. Above a certain range, inequality leads to increased hostility.
Klaus Deininger and Kihoon Lee from the World Bank and Lyn Squire from the Global Development Network provided updated data from the real world to the World Income Inequality Database (WIID) in May 2007. Let us look at processed data (also free download from LuaForge: quick&dirty hack for the scripting language Lua) from that database in order to draw the the range of the Redistributive Aggression (red cluster) and the Plato inequality (blue cluster) plotted over the Gini inequality. From that plot it becomes clear, that the measure for Redistributive Aggression could be an interesting alternative to other existing inequality measures. Below a Gini inequality of 40%, most of the values computed for the Redistributive Aggression are negative.

2008-03-01: From hindsight, I do not feel too comfortable with the term "Redistributive Aggression". Also the term "Inequality Issuization" may overstretch the meaning of the difference between the symmetrized Theil redundancy and the Hoover inequality (inequity) a bit. That difference is information and simply could describe the complexity (or a contribution to that complexity) of managing a given ressource distribution. This complexity then would be zero, if there is an even distribution or around Gini inequalities around 43%. (The 43% - instead of the 47% shown in the previous graph - can be explained by the partitioning of the WIID data: The 43% had been computed based on deciles, where maximum inequality cannot be reached. The 47% had been computed for 2-quantile societies, where the Hoover inequality and the Gini inequality are equal to each other and where maximum inequity can be approached.) The complaxity would have a minimum at Gini inequalities around between 20% and 30%.

World Income Inequality	1960	1970	1980	1989	1998
20% "low"	2.3%	2.3%	1.7%	1.4%	1.2%
60% "middle"	27.5%	23.8%	22.0%	15.9%	9.8%
20% "high"	70.2%	73.9%	76.3%	82.7%	89.0%
Gini	54%	57%	60%	65%	70%
Plato	53%	56%	59%	64%	70%
Symmetric	47%	51%	55%	63%	71%
Hoover	50%	54%	56%	63%	69%
Atkinson	46%	50%	53%	60%	67%
Theil	0.62	0.70	0.76	0.93	1.12
Aggression	0.13	0.17	0.23	0.36	0.54
high : low	30 : 1	32 : 1	45 : 1	59 : 1	74 : 1

38 years of global redistribution:

1960: The poorest 20% of the world's population only had a share of 2.3% of the global income. The top 20% of the world's population earned 70.2% of the global income.
From these data we compute: Gini ≥ 54%, Symmetric ≥ 46%, high/low ≥ 30
(Source: UNDP, 1996)
1998: The poorest 20% of the world's population only had a share of 1.2% of the global income. The top 20% of the world's population earned 89% of the global income.
From these data we compute: Gini ≥ 70%, Symmetric ≥ 71%, high/low ≥ 74
(Source: Intl. Herald Tribune 1999/02/05 pg.6; own estimations 1999/04/03)

Update 2001/11/02 from The No-Nonsense Guide to Globalization (Wayne Ellwood; by the way: he gets 74:1 for 1997.)

After 38 years of globalization income inequality grew significantly, especially after 1980. Associated with growing income inequality is the redistribution of more power to less people. The result is concentration of power - as long as power is mainly determined by economical power. The response to that development is to return to times where power is linked to violence. This is happening right now.

Entropy, Redundancy and Amartya Sen's Complaints:

You won't find a "Theil Redundancy" mentioned elsewhere by economists. Worse, this Web-page is written by an engineer, not by an economist. How come, that the professionals don't use the term "Redundancy" for inequality measures?
If you do not feel comfortable with how entropy is applied to measure inequality, you are not alone: Many people have difficulties to accept, that inequality is "order" and that equality is "disorder". In the first place, one reason for that is, that using the terms "order" and "disorder" is not the best way to explain entropy. One man's order is another man's disorder, which leads to the second point: Is equality good or bad? Is order good or bad? Is inequality good or bad? is disorder good or bad?
But the main reason for the confusion is a simple mistake: An entropy measure like Theil's index is not an entropy, it is a redundancy,. And a redundancy yields a high value for "order", whereas entropy is high for "disorder".
Calling Theil's measure an "entropy" even confused Amartya Sen. From Amartya Sen's "On Economic Inequality" I learned a lot about inequality measures. But entropy seems not do go down too well with him (1973) and his co-author James E. Foster (1997). When describing the "interesting" "Theil entropy" (chapter 2.11), Sen sees a contradiction between entropy being a measure of "disorder" in thermodynamics and entropy being a measure for "equality". If you assume that equality is "order" and thus a antonym for "disorder", then you may believe - Sen even calls it a "fact" - that the Theil coefficient is computed from an "arbitrary formula". However, there is no contradiction: As you know by now, the Theil index is a redundancy. That is the answer to Sen's objection! High equality (high "disorder", if you want to stick to that) leads to a low redundancy and high entropy, whereas high inequality (high "order") leads to a low entropy and high redundancy. Equality is maximum entropy, because it is inequality which to achieve requires an ordering process with effort.
Sen and Foster had another complaint. They didn't think, that Theil's index really yields to "intuition". It may help to remember, that the Theil index (I prefer to call it Theil redundancy) is 0% for a 50%:50% distribution and close to 100% for an equivalent to the (in)famous 80%:20% distribution.

Recommendations:

Coulter^[14] has collected about 50 inequality measures. There probably are a few more. In my calculus you find a collection of selected measures and three "own" ones (1995: Symmetric (then erronously attributed to Kullback-Leibler, better call the redundancy symmetrized Theil redundancy and call the Symmetric inequality symmetrized Theil inequality), 2004: Plato, 2007: Redistributive Aggression). Which one to use? As complexity of computation is no criterion anymore, mainly the significance of an inequality measure determines its importance.
- Simplicity: The simplest inequality measure is the Hoover inequality (also known as Robin Hood Index). It also is the least interpretative one.
- Popularity: But the most popular measure is the Gini inequality. Compute it together with the Plato inequality, which is a pseudo Gini inequality. If the Plato inequality is very different from (e.g. much higher than) the Gini inequality, then you may want to check your quantiles for mistakes or for unusual data.
- Entropy: I favorize entropy measures. To users of the Theil redundancy (usually called Theil index) I recommend to evaluate the Symmetric redundancy (symmetrized Theil redundancy) as an alternative. It is almost as simple, as the Hoover inequality. Substract the Hoover inequality from the Symmetric redundancy in order to compute the Redistributive Aggression (alternatively called Inequality Issuization).
All those indicators are just that: Indicators. They cannot replace reality. These indicators are used to simplify and model reality in order to return to reality with explanations, predictions and decisions. In many cases the meaning of the indicators will be disputed. But especially in a time series, indicators with decreasing or increasing values will make you curious to understand change and the impact of change.
My favorite solution would be to use the Symmetric redundancy. You may hesitate to use this measure, as it theoretically does not have an upper bound. How to interpret values above 100% (above 1)? It is simple: The Symmetric redundancy is 100% for distributions, which are entropywise equivalent to the distribution in a 2-quantiles society of 82:18. That is very close to the "Pareto principle" (80:20). Values below 100% indicate that you are below that "popular" distribution. Values above 100% indicate, that you are above. Use the Symmetric redundancy together with its relative (with regard to the similarity of the formulas) the Hoover inequality (is 100% at maximum inequality). If you prefer all measures to stay between 0% and 100%, then use the Plato inequality (pseudo Gini inequality) instead of the Symmetric redundancy. Also try out, how helpful the Redistributive Aggression (Inequality Issuization) is to you.

Questions:

How much should children be affected by distributional inequality?

Does increased wealth for one subgroup and unchanged wealth for the other subgroups affect the distribution of power within the group?

What is the relation between social entropy and economic entropy?

Sorry for my Germanic English,
Götz Kluge (gk at the domain poorcity.richcity.org), Munich, 2009-09-03, last update: 2021-11-14

www.poorcity.richcity.org,

Footnotes:
[a] The term ln(A_i/E_i) is the unweighted entropy of the quantile_i. Coming from information theory and if A stands for owners and E stands for ressources, then this term can be interpreted as minimum length of the address required to distinguish the owners A per unit ressource E within their quantile. (The base of that length is Euler's constant e. For other bases b you need to devide the entropies by ln(b), e.g. ln(10) or ln(2).) In order to determine, how much entropy this term contributes to the whole system, the term has to be weighted by its share of E, that is E_i/E_total. The sum of the share weighted entropies is the actual entropy of the system: Σ_i=1..N(E_i*ln(A_i/E_i))/E_total. If all A_i/E_i would be same, the entropy would be ln(A_total/E_total), which is the maximum entropy of the system. - As you see, the Theil index (Theil redundancy) is normalized by the ressource unit: E appears as devider. You can read that as "per ressource unit". Now supply siders can start to discuss with demand siders about this property of Theil's index. Alternatively one can use an index which is normalized to a single owner. This is what I call the "liehT redundancy". As in the real world distribution between owners and ressources is mutual, the truth is between both redundancies. That is why I came up with the "Symmetric redundancy". Or call it "symmetrized Theil redundancy". The result is almost as simple and clear as Hoover's inequality.
[b] Euler's constant e≈2.71828 has the property dx/d(e^x)=e^x. To economists that number may look like having originated from physics. Although Euler's constant is very important for physics and first was published by Leonhard Euler in his Mechanica (1736), it was economics where the first few digits of the number were found. Jacob Bernoulli (1654-1705) wrote these digits down when analyzing compound interest, where growth in one step is split into many little growth steps. If the steps become infinitely small, growth is continuous. Examples for an annual interest of 100%: (1) Stepwise growth: 1 Euro grows to 2 Euros in one year if compounding occurs at the end of the year. (2) Deviding one growth step into many little growth steps: 1 Euro grows to about 2.71457 Euros within one year if compounding occurs daily. (3) Continuous growth: 1 Euro grows to about 2.71828 Euros within one year if compounding occurs continuously.

References:
[1] Mark Kesselman: French Local Politics (A Statistical Examination of Grass Roots Consensus), 1966, American Political Science Review, No.60 (December), pg.963-974 (mentioned by Coulter as reference for MacRae coefficient; Daniel MacRae Keenan?)
[2] Lionnel Maugis: Inequity Measures (png) in Mathematical Programming for the Air Traffic Flow Management Problem with En-Route Capacities (for IFORS 96), 1996 (CENA - Centre d'études de la Navigation Aérienne - Sofréavia, Orly Sud 205, 94542 Orly Aérogare Cedex, France)
[3] Redundancy as defined in ISO/IEC DIS 2382-16
[4] William Hanna, Joseph Barbera: The Jetsons (html), 1964-1980
[5] Niklas Luhmann: Die Wirtschaft der Gesellschaft, 1988
[6] Benjamin Barber: Fear's Empire: War, Terrorism, and Democracy, 2003 (Imperium der Angst: Die USA und die Neuordnung der Welt, German translation 2003)
[7] Amartya Sen: On Economic Inequality, 1973 (Enlarged Edition with a substantial annexe after a Quarter Century with James Foster, Oxford 1997)
[8] Yoram Amiel (Autor), Frank A. Cowell: Thinking about Inequality: Personal Judgment and Income Distributions, 2000
[9] Wolfgang Kitterer: Mehr Wachstum durch Umverteilung? (pdf), 2006
[10] Charles I. Jones: Introduction to Economic Growth, 2002 (growth data: Lucas(1998) & Maddison (1995))
[11] Hartmut Bossel: Indicators for Sustainable Development (pdf), 1999
[12] Andreas Kamp, Andreas Pfingsten, Daniel Porath: Do banks diversify loan portfolios? A tentative answer based on individual bank loan portfolios (pdf), Deutsche Bundesbank, 2005
[13] Juana Domínguez-Domínguez, José Javier Núñez-Velázquez: The Evolution of Economic Inequality in tth EU Countries During the Nineties (pdf), 2005 (The authors define a normalized Theil index. That index is similar to the Atkinson inequality given in the calculus above as one of two indices which I found from Atkinson.)
[14] Philip B. Coulter: Measuring Inequality, 1989
[15] Eberhard Schaich: Lorenzkurve und Gini-Koeffizient in kritischer Betrachtung. Jahrbücher für Nationalökonomie und Statistik 185 (1971), 193-298
[16] Károly Henrich: Globale Einkommensdisparitäten und -polaritäten (pdf), 2004
[17] Travis Hale, University of Texas Inequality Project: The Theoretical Basics of Popular Inequality Measures (doc), ≥2003; Examles 1A and 1B
[18] Wikipedia: Theil Index and Hoover Index (html); especially ''The Teil index and the Hoover Index'' and ''Pareto principle'', 2007-10-20 (html)
(Theil-Index in de.wikipedia.org: aktuell und 2007-12-24, interessant auch 2007-11-17)
[19] Michail W. Wolkenstein (Mikhail Vladimirovich Volkenstein): Entropie und Information, Moskau 1986 (excellent explanation of entropy, but out of print)
[20] Arieh Ben-Naim: Entropy Demystified, 2007 (The book keeps the promise of its title and makes science beautiful.)
[21] Nicholas Georgescu-Roegen: Energy and Economic Myths: Institutional and Analytical Economic Essays, 1977
[22] Rainer H. Rauschenberg: Die Bedeutung des zweiten Hauptsatzes der Thermodynamik für die Umweltökonomie (html| zip| pdf), 1990

Links: Calculator (in English) | Rechner (in Deutsch) | Archive (password required) | Lua (4M, for Windows^TM, with Expat and lots of docu)

Keywords: www.poorcity.richcity.org, Gini coefficient, Gini index, inequity measures, income distribution, wealth distribution, concentration measures, statistics, econometrics, welfare function, welfare economy, powerty, wealth, online-calculator, calculus, Pareto distribution, 80:20, 80/20, progressive tax, distributive justice, egalitarism, egalitary; www.umverteilung.de, Pseudo Gini Index, Ginikoeffizient, Theilmaß, Ungleichverteilung, Ungleichheit, Einkommensverteilung, Vermögensverteilung, Konzentrationsmaße, Statistik, Ökonometrie, Wohlfahrtsfunktion, Wohlfahrtsökonomie, Teilhabe, Armuts- und Reichtumsbericht, Umverteilungsdruck, Armut, Wohlstand, Reichtum, Formelsammlung, Online-Rechner, Lorenz-Kurve, Quantile, Platon, Pareto-Verteilung, Steuerprogression, Verteilungsgerechtigkeit, Ergebnisgerechtigkeit, Leistungsgerechtigkeit, Diskussion um die Neidgesellschaft und Gleichmacherei, Egalitarismus, egalitär, Sozialquote, Chancengleichheit, Managergehälter, Einkommensentwicklung, Verteilungsbericht, Durchschnittseinkommen vs. Median, Redundanz, Entropiemaße, Ungleichheitsthematisierung (Inequality Issuization), Ursachen des Terrorismus, Boltzmann-Shannon-Entropy