kurz & knapp |
Anmerkungen |
inequality measures |
spreadsheets |
comparison
"Die Vermögensverteilung in Deutschland weist eine beträchtliche
Disparität auf. Tendenziell nimmt diese seit geraumer Zeit zu, wie
ein Vergleich der EVS-Daten von 1973, 1978, 1983 und 1988 zeigt. (Die Ergebnisse
der EVS von 1993 sind mit früheren EVS-Daten nur eingeschränkt
vergleichbar). Die Reichen sind reicher geworden, weil sie ihr Geldvermögen
durch ansehnliche Vermögenserträge aufstocken konnten. Doch auch
die unterschiedliche Entwicklung der funktionellen Einkommen hat zur Zunahme
der Disparität in der Vermögensverteilung beigetragen: 1996 waren
die entnommenen Gewinne und Vermögenseinkommen mehr als dreimal, die
Nettolohn- und -gehaltsumme aber nur doppelt so hoch wie 1980."
DIW, 1998 (für Einkommen vgl. LIS)
"... in einem freien Volke, wo die
Sklaverei verboten ist, [besteht] der sicherste Reichtum in einer großen
Menge schwer arbeitender Armer. Denn ... ohne sie [würde] es keinen
Lebensgenuss geben, und kein Erzeugnis irgendeines Landes hätte
mehr einen Wert. Um die Gesellschaft glücklich und die Leute selbst
unter den niedrigsten Verhältnissen zufrieden zu machen, ist es
notwendig, dass ein beträchtlicher Teil davon sowohl unwissend
wie auch arm sei. Kenntnisse vergrößern und vervielfachen
unsere Bedürfnisse, und je weniger Dinge ein Mensch begehrt, um so
leichter kann er zufriedengestellt werden."
Bernard de Mandeville, 1714
Die Mathematik der Ungerechtigkeit
Götz Kluge, München, 2000/07/29
bis Ts
DM/Jahr
| Steuer-
zahler | Mio DM
Einkünfte | Mio DM
Steuer |
|
| 5 | 1145008 | 2954 | 16 |
| 10 | 1274868 | 9680 | 97 |
| 15 | 1489169 | 18586 | 393 |
| 20 | 1309984 | 22810 | 983 |
| 25 | 1227877 | 27624 | 1801 |
| 30 | 1333681 | 36714 | 3031 |
| 40 | 3136635 | 110401 | 11804 |
| 50 | 3619401 | 162869 | 20061 |
| 60 | 3105688 | 170061 | 22404 |
| 75 | 3252768 | 217927 | 31404 |
| 100 | 3383398 | 291369 | 46822 |
| 250 | 3126897 | 420419 | 87005 |
| 500 | 207672 | 68629 | 22789 |
| 1000 | 49031 | 32752 | 12924 |
| 2000 | 13820 | 18659 | 7751 |
| 5000 | 5249 | 15461 | 6490 |
| 10000 | 1247 | 8458 | 3467 |
| mehr | 686 | 14801 | 5969 |
|
| Summe | 27683079 | 1650177 | 285211 |
|
Verteilung der Einkünfte in Deutschland (West) 1995
Quelle: Statistisches Bundesamt, Jahrb.1999, 20.10.4
Siehe auch
inequality-1.3.4 und Lorenzkurve.
Für 2001
gibt es ein neues Spreadsheet:
FTcalc-2001.
(2005-12-03)
|
Verteilungsbericht:
Noch in der vergangenen Legislaturperiode (13) wehrte sich
die alte Bundesregierung (CDU/CSU, FDP)
gegen eine verbesserte Berichterstattung
über die Verteilung von Einkommen und
Vermögen in Deutschland (Arbeitstitel im Bundestag: "Verteilungsbericht"):
"Das vorhandene statistische Material zur Einkommens-
und Vermögensverteilung in der Bundesrepublik Deutschland
ist vollkommen ausreichend. Wir brauchen in unserem Lande nicht
mehr Bürokratie, mehr Zahlenakrobatik, mehr
statistische
Spielereien - sondern weniger!" Mit diesen Worten brachte
Heinz-Georg Seiffert (MdB (CDU), 1997/06/13) das Thema
im Bundestag weit unter Stammtischniveau. Eine noch dümmere Reaktion kam dann noch von Wolfgang Kubicki (FDP, Pressemeldung Nr.220/98, Kiel 1998/09/04).
Es reicht wohl schon, Verteilungen nur untersuchen zu wollen, um sofort als
sozialneidisch abgestempelt zu werden. Denken durch Reflexe zu ersetzen kann jedoch schälich sein: Es gibt auch Forscher, die keine Zunahme der Ungleichheit der Einkommen in Deutschland vermuten, aber auch das Fehlen einer guten Datenbasis beklagen. (In den "alten" Bundesländern nahm die Ungleichverteilung der Einkommen von 1992 bis 1995 tatsächlich auch etwas ab. Was bedenklich bleibt, ist die wachsende Ungleichheit der Vermögensverteilung.)
Die alte Opposition (Grüne, PDS, SPD) beklagte sich
über den damaligen Widerstand der alten Regierung. Jetzt könnten zwei der ehemaligen Oppositionsparteien ihre Vorstellungen umsetzen. Ob sie das schon vergessen haben? Möglicherweise will insbesondere die SPD ihre Forderungen nun schnell vergessen. (Bei den Jusos gibt es allerdings schon einen Link zu dieser Seite.) Und die Grünen? "Wenn es denn so ist, dass wir soviel statistisches Material darüber haben - offenkundig ist es so verstreut und schwer zugänglich, dass wir alle uns nicht darauf verständigen können -, dann kann es ja nicht so
schwierig sein, das Ganze zu einem Bericht zusammenzufassen." (Andrea Fischer, 1997/06/13, Plenarprotokoll 13/182)
Inzwischen wird wieder ein "Reichtumsbericht" gefordert. 1998 hatte die SPD ihn in ihrem Wahlprogramm versprochen. Arbeitsminister Riester will ihn Anfang 2001 vorlegen.
Eine Konzept- und Umsetzungsstudie hatte das
Bundesministerium fr Arbeit und Sozialordnung (BMA) beim Institut für
Sozialforschung und Gesellschaftspolitik GmbH (ISG) in Auftrag gegeben (AWO magazin, 2000/01/06).
Das Ergebnis kann man in der Liste der Forschungsberichte des BMA finden : Nr.278 (1999/10). Auch interessant: Nr.260 (1996/12) und Nr.279 (1999/12).
Dazu mache ich hier einen konkreten Vorschlag, wie SPD und Grüne zeigen können, dass ihre Unterstützung für eine Verbesserung des Verteilungsberichtes ernst gemeint war. Der "Reichtumsbericht" (sachlicher wäre "Verteilungsbericht") ist mit einfachen (und in der Ökonometrie akzeptierten) Kennzahlen auszustatten:
- Zu den Einkommensstabellen wird in Zukunft jährlich der symmetrische Ungleichverteilungs-Index (bzw. MacRae-Index, oder Kennzahlen nach Gini, Hoover, Atkinson, Theil usw.) für die Ungleichverteilung der Einkommens- und Vermögensverteilung angegeben.
- Die Wohlfahrtsfunktion (Foster & Sen) wird gleichrangig mit konventionellen Daten (z.B. BIP) jährlich ausgewiesen.
[Anmerkung 2001/04/25: Versprochen und gehalten, Gratulation. Der
Armuts- und Reichtumsbericht der Bundesregierung ist ein Lehrstück geworden.
Damit wird ein großer Teil meiner Kritik (in diesem Text aus dem Jahr 2000) hinfällig.
Übrigens: Jetzt werden neben den Kennzahlen nach Gini auch die nach Atkinson verwendet. Die Angabe der Wohlfahrtsfunktion gleichberechtigt neben dem BSP kommt hoffentlich auch noch.]
[Anmerkung 2003/12/29:
Mit seinem Verteilungsbericht 2003
lieferte der DGB jetzt schon eine Vorlage.
Auf Probleme des Gini-KoeffKennzahlenizienten gehen die Gewerkschaftler nicht ein.
Ich nehme an, dass der Bericht der Bundesregierung 2004 besser wird.]
[Anmerkung 2004/07/03: Mit dem nächsten Verteilungsbericht ist etwa Anfang 2005 zu rechnen.]
[Anmerkung 2004/07/24: Früher empfahl ich den Atkinson-Index. Der ist aber asymmetrisch.
Besser ist der symmetrische Index.]
[Anmerkung 2005/12/03: Für 2001 gibt es ein neues Spreadsheet:
inequality2001germany.
[Anmerkung 2007/07/08: (1) Die symmetrische Redundanz bzw. den symmetrierten Atkinson-Index hatte ich fälschlicherweise Kullback-Leibler zugeordnet. Das ist hier nun abgeändert worden.
(2)Meine alten Ungleichheitsseiten habe ich jetzt allergrößtenteils in ein geschütztes Archiv verschoben. (Darum werden jetzt viele Links auf dieser Seite ins Leere führen.) Wer daran interessiert ist, kann mir ja eine Email schreiben.]
Das vorhandene statistische Material zur Einkommens- und Vermögensverteilung in der Bundesrepublik Deutschland ist nicht ausreichend, denn über die Einkommensverteilung wird nur alle drei Jahre ausführlich berichtet. Auch ist die Aufbereitung der Daten zur Einkommensverteilung für die Öffentlichkeit mangelhaft: Ungleichheitskoeffizienten fehlen. Diese gehören zusammen mit den Tabellen zur Einkommensverteilung in den preiswerten "Zahlenkompass" (und in die Webseiten) des Statistischen Bundesamtes.
Wie kann die Darstellung der Ungleichverteilung so erfolgen, dass sie in einer Zeitreihe
über die Jahre aufgezeigt werden kann? Die Antwort kommt aus den USA (mit in Europa entwickelten Verfahren): Eine wichtige Aussage der nicht nur für Abgeordnete verwirrend vielen Zahlen in der Tabelle wird mit einem geeigneten Ungleichverteilungskoeffizienten knapp
in einer Zahl zusammengefasst. In den USA nimmt man den alten Gini-Koeffizienten. Ich empfehle den DRUK, einen aus der symmetrischen Redundanz abgeleiteten Ungleichverteilungskoeffizienten. (Wem das zu unheimlich ist, kann bei Gini bleiben. Das ist immer noch besser als garkeine Darstellung der Ungleichverteilung.)
Das US Census Bureau fürchtet schon seit einem halben Jahrhundert nicht mehr,
mit der jährlichen Bekanntgabe von Ungleichverteilungskennzahlen den Kapitalismus zu gefährden.
In Deutschland fehlen Indikatoren für die Ungleichverteilung des Einkommens und des Vermögens.
Beispiel: In Sektion 20.10.4 des deutschen statistischen Jahrbuches 1999 finden wir
eine Einkommenstabelle für 1995 mit Aufteilung in Einkommensklassen mit absoluten Grenzen.
Daraus ließen sich z.B. 4 Ungleichverteilungskoeffizienten für 1995 berechnen (brutto und netto, Werte für 1992 in Klammern):
Das Brutto-Einkommen (einschließlich Lohnnebenkosten) sollte berücksichtigt werden, weil es in einem demokratischen Staat das verfügbare Einkommen ist. (Soweit der Einzelne nicht unmittelbar über alle Einkommensanteile verfügt, liegt es an ihm als Wähler, über die Verwendung seiner Steuern und Abgaben mittelbar zu entscheiden.) Das frei verfügbare Netto-Einkommen sollte aber auch beobachtet werden, um die Verteilung unmittelbar anwendbarar Kaufkraft beurteilen zu können.
 Die Mitglieder der jetzigen Regierung haben immer noch
ihre eigenen Forderungen aus der letzten Legislaturperiode umzusetzen.
Konkret geschähe das, wenn die Entwicklung der Ungleichverteilung von
Einkommen und Vermögen in die
Zeitreihen des
statistischen Bundesamtes aufgenommen würden.
(Da auch das dem Bürger zur Beurteilung der Leistungen
der Regierung dient, sollten für der Zugang zu diesen Daten keine Gebühren
erhoben werden.)
Außerdem wäre eine zügigere und jährliche
Berichterstattung besser - wie in den USA. Eine von der Einkommensentwicklung
unabhängige Aufteilung in 10 Dezile plus zusätzlich 2 Quantile für
die Top 5% und Top 1% entspräche der Berichterstattung des
Congressional Budget Office in den USA.
Die Mitglieder der jetzigen Regierung haben immer noch
ihre eigenen Forderungen aus der letzten Legislaturperiode umzusetzen.
Konkret geschähe das, wenn die Entwicklung der Ungleichverteilung von
Einkommen und Vermögen in die
Zeitreihen des
statistischen Bundesamtes aufgenommen würden.
(Da auch das dem Bürger zur Beurteilung der Leistungen
der Regierung dient, sollten für der Zugang zu diesen Daten keine Gebühren
erhoben werden.)
Außerdem wäre eine zügigere und jährliche
Berichterstattung besser - wie in den USA. Eine von der Einkommensentwicklung
unabhängige Aufteilung in 10 Dezile plus zusätzlich 2 Quantile für
die Top 5% und Top 1% entspräche der Berichterstattung des
Congressional Budget Office in den USA.
Der Titel "Die Mathematik der Ungerechtigkeit" ist zugegebenermaßen
etwas provokativ. Ungleichverteilung ist ja nicht notwendigerweise
gleich Ungerechtigkeit. Ein Zusammenhang zwischen beiden besteht darin, dass
eine Wertung zwischen Gerechtigkeit und Ungerechtigkeit
voraussetzt, dass wir auch die Ungleichverteilung beobachten und messen.
Einige Werkzeuge dazu finden Sie in diesem Beitrag.
Welcher der hier oder andernorts vorgeschlagenen
Indikatoren für Ungleichheit der "Richtige" ist, ergibt sich
letztendlich aus seiner Anwendbarkeit in der Praxis, z.B. aus seiner Eignung
als Parameter in möglichst einfachen Modellen, die sich bei Vorhersagen
z.B. in der Kriminologie
(Oliver Cott, Corinna Krohn, Frank Richter), bei Finanzbehörden (Kim M. Bloomquist, IRS), in der Wirtschaft, in der Konfliktforschung usw. bewähren müssen.
Beispiel: Ungleichverteilungskoeffizienten lassen sich sowohl für Einkommensverteilungen wie auch für Vermögensverteilungen berechnen. Wie man Ungleichverteilung berechnet, zeigt der folgende Beitrag anhand der Verteilung eines "Gesamtvermögens" von etwa 10 Billionen Mark in Deutschland (1995). In der Bundestagsdrucksache 13/7828 finden wir dazu Angaben von der SPD, aus der sich die folgende Verteilung ergibt:
A=Leute E=Vermögen
Klasse 1: 50% besaßen 2,5%
Klasse 2: 40% besaßen 47,5%
Klasse 3: 9% besaßen 27,0%
Klasse 4: 1% besaßen 23,0%
Aus einer derartigen Vermögensverteilung werden wir verschiedene Ungleichverteilungskoeffizienten berechnen. (Die im folgenden Text ermittelten Koeffizienten sind übrigens "freundlich". Die tatsächlichen Ungleichverteilungen werden sogar noch größer sein als die errechneten, denn die Ungleichverteilung innerhalb der Klassen kann mangels Daten hier nicht berücksichtigt werden.)
In einem ersten Schritt stellen wir die Daten "normalisiert" dar:
A1 = 0,50 E1 = 0,025
A2 = 0,40 E2 = 0,475
A3 = 0,09 E3 = 0,27
A4 = 0,01 E4 = 0,23
"Normalisieren" ist die Umwandlung absoluter Werte in auf eine Norm bezogene Werte. Wenn auf die Zahl Eins normalisiert wird, dann ist die Eins die Summe der normalisierten Werte in jeder Spalte unserer Eingangsdaten.
Eigentlich sind Daten bereits auf Eins normalisiert, weil die Werte in Prozent vorliegen. Denn 1=100%. Der Einheitlichkeit halber quetsche ich alle Werte hier deutlich sichtbar in den Bereich zwischen Null und Eins.
(Es gibt platzsparendere Rechenmethoden, die erst beim Resultat eine Normalisierung vornehmen. Aus didaktischen Gründen normalisiere ich hier jedoch bereits die Eingangsdaten.)
Hoover-Ungleichverteilungskoeffizient (HUK): Mit den normalisierten Daten können wir nun ganz schnell schon einen ersten Ungleichverteilungskoeffizienten berechnen.
D1 = E1 - A1 = -0,475 abs(D1) = 0,475
D2 = E2 - A2 = 0,075 abs(D2) = 0,075
D3 = E3 - A3 = 0,180 abs(D3) = 0,180
D4 = E4 - A4 = 0,220 abs(D4) = 0,220
Summe = 0,000 Summe = 0,950
HUK = Summe(abs(D))/2 = 0,475 = 48%
Anmerkung: Eine Alternative zu Summe(abs(D))/2 ist die Summe aller positiven D.
Summe(abs(D))/2 ist jedoch in Spreadsheets einfacher zu realisieren.
Die Summe aller Disparitäten D haben wir nur zur Kontrolle berechnet: Sie muss Null sein. Für den HUK brauchten wir die Summe der vorzeichenlosen Beträge der einzelnen Klassen-Disparitäten. Er ist gleich der Hälfte dieser Summe.
Was ist eine Klassen-Disparität? Wenn das Gesamtvermögen gleichverteilt wäre, dann müsste zum Beispiel die Klasse 1 einen Anteil von 0,5 am Gesamtvermögen haben, denn sie hat auch einen Anteil von 0,5 an der Bevölkerung. Tatsächlich besitzt diese Klasse aber nur eine Anteil von 0,025 des Gesamtvermögens. Die Diskrepanz ist also -0,475.
Die Summe der Beträge aller Klassen-Disparitäten D ist der doppelte Anteil am Gesamtvermögen, der umverteilt werden müsste, wenn man eine völligen Ausgleich erreichen wollte. Sie ist ist deswegen der doppelte Anteil, weil er sowohl die Summe aller abzugebenden Beträge wie auch die Summe aller zu empfangenden Beträge enthält. Weil sie der doppelte Anteil ist, teilen wir sie durch Zwei um den HUK zu berechnen.
symmetrische Redundanz (symR): Die symR ist verwandt mit dem HUK.
ln(E1/A1)×D1 = 1,4230
ln(E2/A2)×D2 = 0,0129
ln(E3/A3)×D3 = 0,1978
ln(E4/A4)×D4 = 0,6898
Summe = 2,3234
symR = Summe(ln(E/A)×D)/2 = 1,1617
Anmerkung: y=ln(x) ist die Umkehrung von x=ey=exp(y), e=2,71828183...
Die Klassen-Disparitäten D=E-A werden hier nicht mit der
abs()-Funktion ihres Vorzeichens beraubt, sondern sie werden durch die
Multiplikation mit ln(E/A) zu positiven Zahlen, denn E-A und ln(E/A)=ln(E)-ln(A)
haben immer das gleiche Vorzeichen. (Das Produkt von Zahlen mit gleichem Vorzeichen ist
niemals negativ.) Gleichzeitig gewichtet
diese Multiplikation die Klassen-Disparitäten mit der wirtschaftlichen
Macht der Klasse, zu der sie gehören: E/A ist proportional zum Einkommen pro Person.
Der Logarithmus[1] ln(E/A) ist wiederum proportional zur Länge der Zahl,
die sich aus E/A ergibt. Damit ist (E-A)×ln(E/A) das Produkt aus
der Disparität für eine Klasse und aus dem Umverteilungsdruck[2]
dieser Klasse. (Für jede Klasse gibt es ein solches Produkt. Die Häfte
der Summe aller dieser Produkte ist die symR.)
Die symR ist mir auch als "Kreuz-Entropie" begegnet. Aber in der Entropiedomäne gibt es drei
Größen, die wir sauber auseinanderhalten müssen. Einmal ist das die
Entropie selbst. Dann gibt es noch die Negentropie, die nichts anderes ist, als negative
Entropie. Schließlich gehört die Redundanz als Differenz zweier Entropien
ebenfalls in die Entropiedomäne.
- Entropien
(H) sind Ordnungsverlustfaktoren. Sie sind Null bei totaler Ungleichverteilung (unendlich hohe Konzentration) und sind positiv bei geringerer Ungleichverteilung.
Die Entropie[3] eines Systems hat ihr (positives) Maximum erreicht, wenn im System alle Freiheitsgrade (alle möglichen Systemzustände) "besetzt" sind.
Dann ist das System im Gleichgewicht - also ohne Optionen, ohne Leben.
Im abgeschlossenen System kann die Summe seiner Entropien niemals abnehmen.
Im abgeschlossenen Markt kann die Gleichverteilungen niemals abnehmen.
- Negentropien
(-H) sind Ordnungsgewinnfaktoren. Addiert man sie zu einer Entropie, so wird die Entropie kleiner.
Die Verwendung der "Negentropie" macht eigentlich nur bei offenen Systemen einen Sinn: Anstelle von einem Export von Entropie zu reden, kann man auch von einem Import von Negentropie sprechen.
Da ein System selbst die Summe seiner Entropien niemals verringern kann, kann es nur als offenes System durch den Import von Negentropie gegen das Erreichen seiner maximalen Entropie ankämpfen.
- Redundanzen
(R = Hmax-H) sind Ordnungsreservefaktoren. Sie sind Null bei totaler Gleichverteilung und sind positiv, wenn die Gleichverteilung nicht mehr perfekt ist.
Die Redundanz[4] eines Systems hat ihr (positives) Maximum erreicht, wenn im System kein Freiheitsgrad (keiner der möglichen Systemzustände) "besetzt" ist.
Die aktuelle Redundanz eines Systems ist gleich der maximalen Entropie des Systems abzüglich der aktuellen Entropie (oder zuzüglich der aktuellen Negentropie) des Systems.
Offene Systeme können ihre Redundanz durch einen ausreichenden Export von Entropie (bzw. Import von Negentropie) steigern oder zumindestens erhalten. Wir leben nicht im Überfluss, sondern vom Überfluss.
Im abgeschlossenen System kann die gesamte innere Redundanz (der Überfluss) niemals zunehmen.
Im abgeschlossenen Markt kann die Ungleichverteilungen niemals zunehmen.
Angesichts ihres Verhaltens und ihres Zustandekommens befindet sich die symR zwar in der
Entropiedomäne[5], ist aber keine Entropie, sondern eine Redundanz.
Zu ihrer Berechnung werden pro Klasse Ausdrücke mit der Struktur ln(E/A)×D = (ln(E)-ln(A))×(E-A) aufsummiert.
Hierbei ist (E-A) die normalisierte Disparität in einer Klasse und (ln(E)-ln(A)) repräsentiert den mit der Disparität verbundenen normalisierten Organisationsaufwand, der
um so leichter aufgebracht werden kann, desto höher der Umverteilungsdruck in dieser Klasse oder auf diese Klasse ist.
Redundanz
R | Gleichverteilung
1-Z | Ungleichverteilung
Z |
|
| 0 × ln(2) | 1 | 0 |
| 1 × ln(2) | 0.5 | 0.5 |
| 2 × ln(2) | 0.25 | 0.75 |
| ... | ... | ... |
| R | exp(-R) | 1-exp(-R) |
|
|
ln(2) ist ungefähr 0,69315
|
Redundanzen (z.B. die symR) können aus der Entropiedomäne in die Verteilungsdomäne transformiert und dort als Ungleichverteilungskoeffizienten (z.B. der DRUK, siehe unten) dargestellt werden. Den Zusammenhang zwischen Redundanzen R und Ungleichverteilungskoeffizienten Z veranschaulicht die linksstehende Tabelle. Hier gilt: Z=1-exp(-R).
Die symR beschreibt, wie inhomogen zwei Stoffe miteinander vermischt sind, d.h. - etwas grob gesagt - wie "ordentlich" zwei Stoffe voneinander getrennt sind, wieviel Platz (Redundanz) also noch für eine gleichverteilende Vermischung bleibt. Die symR gilt für Systeme, in denen sowohl E (z.B. Vermögen) wie auch A (z.B. Leute) Klassenbarrieren durchdringen können. Wenn alle E und A sich rein zufällig und den Naturgesetzen gleichmäßig unterworfen in einem isolierten Raum bewegten, dann ergäbe sich langfristig "von selbst" totale Gleichverteilung. Wegen der Zufälligkeit nenne ich das "Unordnung" im Gegensatz zu "Ordnung", die nicht "von selbst" entsteht. Aufräumen bedeutet, freien Platz zu schaffen - unbelegten Platz, redundanten Platz.
Wenn (abgesehen von zufälligen Fluktuationen) Ungleichverteilung entsteht (z.B. wenn gleichmäßig verteiltes Gerümpel in der Spielkiste konzentriert wird, wodurch unbelegter Freiraum entsteht), muss irgendeine "ordnende Hand" die Isolation des Raumes von außen durchbrochen und diese Ordnung (Ungleichverteilung) herbeigeführt haben, denn in einem isolierten System kann die Summe aller Entropien nicht "von selbst" absinken. Darum kann die Summe aller Redundanzen (die Summe aller ungenutzten Freiräume) nicht "von selbst" ansteigen.
Die symR beschreibt ungleiche Zuordnung von Resourcen zu Menschen als Entropiemaß - ohne jedoch Menschen mit irgendwelchen in der Physik willenlos umherschwirrenden Partikeln[6] gleichzusetzen. Es gibt einen Unterschied zwischen Vergleich und Gleichsetzung: Entropiemaße beruhen nicht auf einer technokratischen Gleichsetzung von Gesellschaft mit Molekülen in idealen Gasen, sondern sie drücken durch einen Vergleich gerade den Unterschied zwischen sozialen (willenbehafteten) und physikalischen (willenlosen) Systemen aus, damit auch zwischen Selbstbestimmung und Fremdbestimmung.[7]
D&R-Ungleichverteilungskoeffizient (DRUK, D=Demand und R=Reserve):
Ungleichverteilungskennzahlen in der (für Redundanzen nach oben offenen) Entropiedomäne sind allerdings für viele Menschen nicht so einfach intuitiv zu begreifen. MacRae transformierte vielleicht auch darum die Theil-Redundanz TR (dazu komme ich später noch) aus der Entropiedomäne in die Verteilungsdomäne (zwischen 0% und 100%). Es entstand der MacRae-Gleichverteilungskoeffizient MGK=exp(-TR). Der MacRae-Ungleichverteilungskoeffizient wäre dann: MUK=1-MGK. Wir machen dasselbe mit der symmetrische Redundanz (symR):
DRUK = 1-exp(-symR) = 0,6870 = 69%
Es gibt übrigens noch einen Weg, wie man den DRUK ohne den Umweg über die symR berechnen kann.
(A1/E1)^D1 = 0,2410
(A2/E2)^D2 = 0,9872
(A3/E3)^D3 = 0,8206
(A4/E4)^D4 = 0,5017
Produkt = 0,0979
DRUK = 1-(Produkt((A/E)^D))^(1/2) = 0,6870 = 69%
Anmerkungen: a^b = ab; Produkt(x) = x1×x2×x3×...×xn
D steht für Nachfrage (Demand), R steht für Reserve: Je höher der DRUK, desto größer werden die Begehrlichkeiten. Im Jahr 1995 war die deutsche Vermögens-Disparität HUK=48%. Der DRUK=69% ist höher. Bei niedrigen HUKs kann es sein, dass der DRUK unterhalb des HUK liegt. Das könnte so interpretiert werden, dass niedrige Disparitäten toleriert werden, sehr hohe Disparitäten dagegen ein Umverteilungsbegehren auslösen, das "über das Ziel hinausschießen" kann.
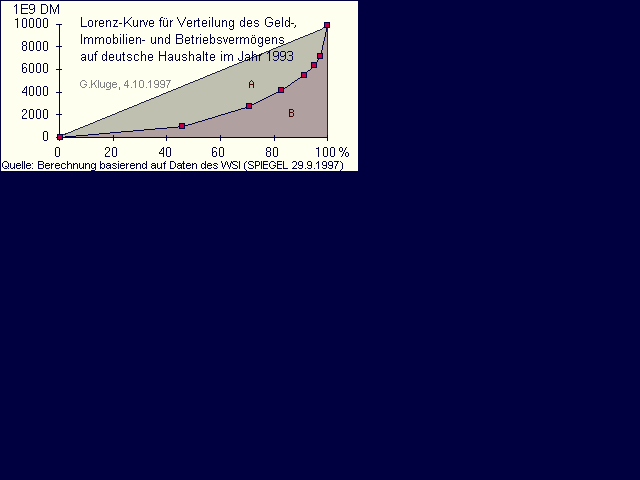 Vermögen[8]: Die Angaben der SPD habe ich gewählt, weil sich damit gut ein einfaches Rechenbeispiel gestalten lässt. Jedoch nach Daten des WSI (SPIEGEL 1997/09/29) ist in Deutschland DRUK=49% für 1993,
also eine geringere Ungleichverteilungen des "Geld-, Immobilien- und
Betriebsvermögens". Man muss sich also die Datenbasis wohl noch etwas genauer ansehen.
Vermögen[8]: Die Angaben der SPD habe ich gewählt, weil sich damit gut ein einfaches Rechenbeispiel gestalten lässt. Jedoch nach Daten des WSI (SPIEGEL 1997/09/29) ist in Deutschland DRUK=49% für 1993,
also eine geringere Ungleichverteilungen des "Geld-, Immobilien- und
Betriebsvermögens". Man muss sich also die Datenbasis wohl noch etwas genauer ansehen.
Einkommen: Für Gesamteinkünfte nach Steuern (1995, Stat. Jahrbuch 1999,
Sektion 20.10.4) ist der DRUK=27%. (USA: DRUK=33% im Jahr 1988.) In sogenannten Niedriglohnländern (z.B. Mexiko) werden wohl Werte um die 50% herum erreicht. (Alle Werte gelten für Verteilungen, die mindestens in Dezile aufgeteilt
sind.) Weltweit ist die Ungleichverteilung des Einkommens innerhalb von 35 Jahren von DRUK=47% (1963) über DRUK=65% (1993) auf DRUK=71% (1998) angestiegen! (Berechnung auf Basis sehr grob unterteilter UNDP-Daten. Tatsächlich wird man bei feinerer Auflösung der Daten zu höheren Ungleichverteilungen kommen.)
Ungleichverteilung ist wegen der damit verbundenen Redundanz nicht unbedingt schlecht. Denn Redundanz zu besitzen bedeutet auch, Reserven zu haben. Ist die Ungleichverteilung 0%, dann bedeutet das schlicht: Es gibt keine Reserven mehr. Etwas in Luxus versteckte Redundanz darf und sollte sich eine Gesellschaft also schon leisten. Wird die Ungleichverteilung jedoch als zu groß empfunden (wie subjektiv das auch immer sein mag), weil zuviele Reserven zusammengehamstert wurden, dann kann es schnell sehr ungemütlich werden: "A perceived sense of inequity is a common ingredient of rebellion in societies" (Amartya Sen, 1973)
Theil-Redundanz (TR): Die Anwendung der symmetrische Redundanz (symR) ist mir bisher nur in der Informationstheorie bekannt. Soziologen werden darum bei der Vorstellung der symR vielleicht etwas gestutzt haben. Aus der Entropiedomäne kennen sie aber die Theil-Redundanz (auch wenn sie das Wort "Redundanz" nicht in diesem Zusammenhang benutzen) und ziehen sie immer häufiger dem ihnen bisher noch geläufigeren Gini-Ungleichverteilungskoeffizienten (GUK, wird später erklärt) vor.
Die symR nimmt Bezug auf Systeme, in denen sowohl E wie auch A die Barrieren zwischen den Klassen durchdringen kann. Bei der TR dagegen ist E wie ein Stoff, der in A gelöst ist. Nur das Lösungsmittel A kann die semipermeablen Barrieren zwischen den Klassen überwinden.
In unserem Beispiel sind A Menschen, die sich willentlich bewegen. E steht für Resourcen, die nicht willentlich bewegen können. Die symR berücksichtigt sowohl willentliche wie auch nicht willentlich beeinflussbare Mobilität in der Osmose, während in dem osmotischen Referenzsystem der TR nur willentliche Bewegungen omnipotenter Menschen erfolgen.
ln(E1/A1)×E1 = -0,0749
ln(E2/A2)×E2 = -0,0816
ln(E3/A3)×E3 = 0,2966
ln(E4/A4)×E4 = 0,7212
TR = Summe = 1,0245
Anmerkung: (TR(E|A)+TR(A|E))/2 = symR(E|A) = symR(A|E)
Die symmetrische Redundanz symR ist der arithmetische Mittelwert der Theil-Redundanz mit vertauschten Eingangsdaten TR(A|E) und der Theil-Redundanz mit unvertauschten Eingangsdaten TR(E|A). Das Ergebnis der symR bleibt bei vertauschten Eingangsdaten unverändert. Je besser die Auflösung ist (z.B. eine feinere Unterteilung in mehr Einkommensklassen), desto näher kommen sich symR und TR.
MacRae-Ungleichverteilungskoeffizient (MUK): Die Theil-Redundanz wird (oft als "Theil-Maß") direkt angegeben. Aber auch hier ist eine Transformation von der nach oben offenen Entropiedomäne in die zwischen Null und Eins liegende Verteilungsdomäne möglich. MacRae hat allerdings nur einen Gleichverteilungskoeffizienten (MGK) erdacht. Der Schritt zum MacRae-Ungleichverteilungskoeffizienten ist aber einfach: MUK=1-MGK, wobei der MUK sich dann als ein sehr enger Verwandter eines der Atkinson-Indizes entpuppt.
MGK = exp(-TR) = 0,3590 = 36%
MUK = 1-exp(-TR) = 0,6410 = 64%
Anmerkung: 1-(MGK(E|A)×MGK(A|E))^(1/2) = DRUK(E|A) = DRUK(A|E)
1-DRUK (Eins abzüglich der D&R-Ungleichverteilung) ist der geometrische Mittelwert der MacRae-Gleichverteilung mit vertauschten Eingangsdaten MGK(A|E) und der MacRae-Gleichverteilung mit unvertauschten Eingangsdaten MGK(E|A). Das Ergebnis des DRUK bleibt bei vertauschten Eingangsdaten unverändert. Je besser die Auflösung ist (z.B. eine feinere Unterteilung in mehr Einkommensklassen), desto näher kommen sich DRUK und MUK.
[9]
Gini-Ungleichverteilungskoeffizient (GUK): Dieser Koeffizient scheint seine Beliebtheit seiner graphischen Anschaulichkeit zu verdanken. Im Gegensatz zu allen anderen Koeffizienten müssen die (E,A)-Paare vorsortiert werden (s.u.).
Der GUK ist eine Auswertung der "Lorenz-Kurve". Diese Kurve entsteht, wenn Sie die untenstehenden (X,Y)-Paare als Punkte in ein karthesisches Koordinatensystem eintragen und sie miteinander verbinden. (Die X-Werte brauchen wir nur zum Zeichnen der Lorenz-Kurve, nicht jedoch zum Berechnen des GUK.)
Die Fläche unter der Kurve nenne ich B (siehe Grafik oben). Bei totaler Gleichverteilung wäre die Kurve eine Diagonale zwischen den Eckpunkten (0/0) und (1/1). Die Fläche unter der Diagonale wäre 0,5 mit normierten Daten (wie wir sie hier verwenden). Dann gilt: für den Gini-Ungleichverteilungskoeffizienten: GUK = (0,5-B)/0,5 = 1-2×B.
Diese Flächenverhältnisse kann man wie folgt berechnen:
E(i) und A(i) müssen so sortiert sein,
dass gilt: E(i)/A(i)>E(i-1)/A(i-1)
Errechnen der Daten für die Lorenz-Kurve:
X0 = 0,000 Y0 = 0,000
X1 = A1+X0 = 0,500 Y1 = E1+Y0 = 0,025
X2 = A2+X1 = 0,900 Y2 = E2+Y1 = 0,500
X3 = A3+X2 = 0,990 Y3 = E3+Y2 = 0,770
X4 = A4+X3 = 1,000 Y4 = E4+Y3 = 1,000
Errechnen des GUK:
(Y1×2-E1)×A1 = 0,0125
(Y2×2-E2)×A2 = 0,2100
(Y3×2-E3)×A3 = 0,1143
(Y4×2-E4)×A4 = 0,0177
Summe = 0,3545
GUK = 1-Summe = 0,6455 = 65%
Empfehlung:
Welche dieser Kennzahlen empfehle ich zur Untersuchung von Ungleichverteilung?
- Hoover-Ungleichverteilung (HUK):
Der HUK ist der einfachste Koeffizient. Er gibt ohne Interpretation an, wieviel umverteilt werden muss, bis Gleichverteilung erreicht wird. Diese Kennzahl ist einfach und unstrittig.
- MacRae-Ungleichverteilung (MUK):
Empfehle ich zur Darstellung der Ungleichverteilung in Meritokratien,
z.B. zur Darstellung der Einkommens- und Vermögensverteilung innerhalb von Unternehmen
oder in Systemen, die sich an einer völlig freien Marktwirtschaft messen.
Der MUK ist eine Transformation der Theil-Redundanz und ähnelt stark einem der Indizes von Atkinson. Die TR ist bereits eine prakisch benutzte Alternative zu Ginis Koeffizienten (GUK), hat aber nicht den Wertebereich des GUK.
Der MUK liegt dagegen genau im Wertebereich des GUK von 0 bis 1 bzw. von 0% bis 100%.
Der MUK beschreibt, wie groß in einer entropiemäßig äquivalenten Zwei-Klassen-Meritokratie
die Klasse ist, die kein Einkommen (bzw. kein Vermögen) kontrolliert.
- Theil-Redundanz (TR):
Die TR (bzw. den MUK) empfehle ich, wenn man sich auf "etablierte" Ungleichverteilungsmaße beschränken will.
- Symmetrischer Index bzw. D&R-Ungleichverteilung (DRUK):
Empfehle ich zur Darstellung der Ungleichverteilung in der politischen Ökonomie. Der DRUK bewertet Ungleichverteilung gemäß den Maßstäben der sozialen Marktwirtschaft.
Der DRUK ist 100%, wenn es Klassen mit Null-Einkommen bzw. Null-Vermögen gibt. (Beispiel: Experimentieren Sie mit dem Wert für das Existenzminimum in EINK1995.WK1 im Spreadsheet-Paket.)
In einem Wohlfahrtsstaat sind Klassen völlig ohne Resourcen ja auch nicht akzeptabel.
Wo dieses Verhalten des DRUK stört, sollten wir uns nicht wieder auf den alten GUK zurückziehen, sondern
den MUK verwenden.
- Symmetrische Redundanz (symR):
Anwendungsbereich wie DRUK, aber vielleicht weniger anschaulich. Für Vergleiche mit Theil-Redundanz geeignet.
- Gini-Ungleichverteilung (GUK):
Sollte nur verwendet werden, wenn Vergleiche zu früheren oder anderen Messungen erforderlich sind, die auch den GUK verwenden.
Wohlfahrt und Marktmacht:
Mit Wohlfahrtsfunktion = (1-MUK) × Volkseinkommen / Bevölkerungsgröße kann man in Anlehnung an James E. Foster and Amartya Sen (On Economic Inequality, "welfare function", S.129) auch eine absolute Einkommensverteilung (pro Kopf) berechnen. Dagegen beschreiben die bisher vorgestellten Kennzahlen nicht die absolute, sondern die relative Ungleichverteilung des Vermögens. Häufig werden sie auch zur Beschreibung der relativen Ungleichverteilung von Einkommen verwendet.
Sen und Foster berechneten die Wohlfahrtsfunktion nicht mit dem DRUK. Sen schlug zuerst den GUK vor, Foster benutzte später den MUK. Wem der DRUK nicht geheuer ist, dem schlage ich zur Berechnung der Wohlfahrtsfunktion auch ersteinmal den MUK - ein Atkinson-Index - vor. Das sieht dann für 1995 so aus: Wir teilen 1650177 Millionen DM durch 27683079 Steuerzahler und bekommen so einen jährlichen Betrag von 59610 DM pro Steuerzahler, also etwa 5000 DM pro Monat an durchschnittlichen Einkünften. Die steckt sich aber nicht Jeder im Monat in die Tasche, denn wir haben ja eine Ungleichverteilung zu berücksichtigen: Der MUK für 1995 ist 33%.
Bei der Berechnung der Wohlfahrtsfunktion stellten sich Sen und Foster im Prinzip nun vor, dass vom Kuchen der gesamten Einkünfte ersteinmal 33% (im Fall unseres Beispiels) als Bonus an Begünstigtere verteilt werden. Die übrig gebliebenen 67% dienen dann als Grundlage für die Berechnung von um den Bonus verminderten durchschnittlichen Einkünften. Dieser für die Verteilung übrig gebliebene Anteil ist die "Wohlfahrtsfunktion": Mit 59610 DM × (1-0,33) errechnen wir pro Steuerzahler eine Wohlfahrtsfunktion von 39938 DM, also etwa 3300 DM monatlich. (Mit dem DRUK berechnet wären das etwa 3400 DM.)
Wir haben hier ein Modell einer aus zwei Klassen bestehenden Gesellschaft (es gibt noch andere Zwei-Klassen-Modelle), in der die Verteilung der Einkünfte sehr einfach strukturiert ist, aber hinsichtlich der Ungleichverteilung 1995 den Verhältnissen der realen Gesellschaft entspricht. Man kann berechnen, wie groß die Klasse der Elite in diesem Fall sein muß. Sie bekommt 100%×Eliteanteil plus 33%×Plebsanteil. Der Rest bekommt nur 67%×Plebsanteil. Nun muss man die zu diesen Einkünften gehörenden Klassengrössen (Eliteanteil und Plebsanteil) so verteilen, dass wieder ein MUK von 33% herauskommt. Das geschieht bei
93,5% Plebsanteil (durchschnittliche Monatseinkünfte: 3300 DM) und
6,5% Eliteanteil (durchschnittliche Monatseinkünfte: über 28000 DM).
Hierdurch wird die Bedeutung der Wohlfahrtsfunktion anschaulich.
Man kann den DRUK auch für die Kaufkraftverteilung berechnen und dann in Anlehnung an die Wohlfahrtsfunktion den durchschnittlichen Einfluß des Einzelnen im Markt ermitteln. Dann ist in Regionen, in denen Marktwirtschaft dominiert, die durchschnittliche Marktmacht pro Kopf = durchschnittliche Kaufkraft pro Kopf × (1-DRUK) mein Vorschlag für eine Kennzahl, mit deren Hilfe sich ersehen läßt, ob ein erreichter durchschnittlicher Kaufkraftzuwachs bei gleichzeitig steigender Ungleichverteilung zu mehr oder zu weniger Macht des Einzelnen im Markt führt. Zum Teil wird schon die Wohlfahrtsfunktion selbst Hilfe geben können, eine gute Kennzahl fr die Bilanz von Gewinnern und Verlierern bei der Einkommens- und Vermögensentwicklung zu bekommen. Das ist nötig, weil bei relativer Betrachtung das Pareto-Kriterium nie erfüllt wird und deswegen immer verliert, wer nicht gewinnt[10].
Literatur:
- Bundestagsdrucksachen zur Forderung nach einem "Reichtumsbericht":
14/999,
14/1069,
14/1213
- Forschungsberichte des BMA: Nr.278 (1999/10). Auch interessant: Nr.260 (1996/12) und Nr.279 (1999/12)
- frühere Bundestagsdrucksachen:
13/6527 (Dr. Gregor Gysi und Gruppe),
13/7606 (Detlev von Larcher, Hans-Georg Seiffert),
13/7828 (Konrad Gilges u.A),
13/7933 (Rudolf Scharping und Fraktion),
Plenarprotokoll 13/182 13.06.97 (Redner: Dieter Grasedieck, SPD; Heinz-Georg Seiffert, CDU; Andrea Fischer, Bündnis 90/Die Grünen; Dr. Barbara Höll, PDS)
- Statistisches Jahrbuch 1999 (1998), Sektion 20.10.4, Gesamteinkünfte 1995 (1992) nach Steuern
- Pedro Conceiçã / James K. Galbraith: Constructing Long and Dense Time-Series of Inequality, 1999? (Gute Erklärung des Theil-Maßes)
- Philip B. Coulter: Measuring Inequality, 1989
- Deutscher Gewerkschaftsbund (DGB) und der Paritätischer Wohlfahrtsverband (DPWV): Armutsbericht, 2000/10
- Hans-Peter Dürr: Selbstbeschränkung - eine unmögliche Notwendigkeit, Kommune 1998/10
- Thomas Byrne Edsall: The Return of Inequality, Atlantic Monthly, June 1988
- James K. Galbraith: Created Unequal, 1998
- Christian Hein
(WOCATE): Entropie - eine Zugangsgröße zur Herausbildung allgemeinen Technikverständnisses?, Halle 1997, (wenn wieder mal aus dem WWW
genommen, hier die Mirror-File: ENTHEIN.ZIP)
- F.Hengsbach SJ / M.Möhring-Hesse: Aus der Schieflage heraus (Demokratische Verteilung von Reichtum und Arbeit), 1999, ISBN 3-8012-0278-X
- Uwe Jean Heuser: Die neue Teilung, Wohlstand für wenige, DIE ZEIT 1997/10/24
- Ernst-Ulrich Huster (Hg.): Reichtum in Deutschland (Die Gewinner der sozialen Polarisierung), 1997
- ISO/IEC DIS 2382-16, Information theory (Definition von Entropie, Negentropie und Redundanz für die Informationstheorie)
- Mark Kesselman: French Local Politics, 1966, American Political Science Review, No.60, S.963-974 (Anwendung des MacRae-Koeffizienten)
- Hartmut Köhler: Mathematics Teaching and Democratic Education, Stuttgart Institute for Education and Learning, D-70174 Stuttgart (empfohlen von Colin Hannaford, New Scientist 1999/08/28, S.46)
- Solomon Kullback: Information Theory and Statistics, 1997
- Lutz Leisering / Stephan Leibfried: Time and Poverty in the Welfare State, 1999 (2000?) (Übersetzte und dabei intensiv überarbeitete Ausgabe von "Zeit der Armut", 1995)
- Lionnel Maugis: Inequality Measures, 1996
- M. Marsh M. / D. Schiling: Equity measurement in facility location analysis (a review and framework), European Journal of Operational Research, 7(1):1-17, April 1994 (Anwendung des Hoover-Koeffizienten)
- Werner Rügemer: Arm und reich, 2002, ISBN 3-933127-92-0
- Eberhard Schaich: Lorenzkurve und Gini-Koeffizient in kritischer Betrachtung, Jahrbücher für Nationalökonomie und Statistik 185 (1971), S.193-298
- E. Schroedinger: What is life? 1943 (Schrödinger: Was ist Leben?, 1987)
- J.A.Schumpeter: Capitalism, Socialism and Democracy, 1942; Kapitalismus, Sozialismus und Demokratie, 1946, ISBN 3-8252-01720-4
- Amartya Sen, James E. Foster: On Economic Inequality, 1973/1997
- SPD Wahlprogramm 1998: Soziale Sicherheit und Gerechtigkeit (Versprechen eines nationalen Armuts- und Reichtumsberichts)
- UNDP: http://www.undp.org/hdro/e96over.htm, 1996
- Universität Konstanz: Datenquellen
- US Census Bureau: Income Inequality, http://www.census.gov/hhes/www/incineq.html
- Beate Willms, Winfried Roth Darüber spricht man nicht, TAZ-magazin, 1999/08/21
- Edward N. Wolff: Top Heavy, 1995
- Michail W. Wolkenstein: Entropie und Information, Moskau 1986
- Karl Georg Zinn: Wie Reichtum Armut schafft, 1998, ISBN 3-89438-150-7
Götz Kluge
Albany (NY) 1997/10/27; München 2000/09/10; München 2007/07/08 (Kullback-Leibler gegen "symmetrisch" ausgetauscht)
 Die Mitglieder der jetzigen Regierung haben immer noch
ihre eigenen Forderungen aus der letzten Legislaturperiode umzusetzen.
Konkret geschähe das, wenn die Entwicklung der Ungleichverteilung von
Einkommen und Vermögen in die
Zeitreihen des
statistischen Bundesamtes aufgenommen würden.
(Da auch das dem Bürger zur Beurteilung der Leistungen
der Regierung dient, sollten für der Zugang zu diesen Daten keine Gebühren
erhoben werden.)
Außerdem wäre eine zügigere und jährliche
Berichterstattung besser - wie in den USA. Eine von der Einkommensentwicklung
unabhängige Aufteilung in 10 Dezile plus zusätzlich 2 Quantile für
die Top 5% und Top 1% entspräche der Berichterstattung des
Congressional Budget Office in den USA.
Die Mitglieder der jetzigen Regierung haben immer noch
ihre eigenen Forderungen aus der letzten Legislaturperiode umzusetzen.
Konkret geschähe das, wenn die Entwicklung der Ungleichverteilung von
Einkommen und Vermögen in die
Zeitreihen des
statistischen Bundesamtes aufgenommen würden.
(Da auch das dem Bürger zur Beurteilung der Leistungen
der Regierung dient, sollten für der Zugang zu diesen Daten keine Gebühren
erhoben werden.)
Außerdem wäre eine zügigere und jährliche
Berichterstattung besser - wie in den USA. Eine von der Einkommensentwicklung
unabhängige Aufteilung in 10 Dezile plus zusätzlich 2 Quantile für
die Top 5% und Top 1% entspräche der Berichterstattung des
Congressional Budget Office in den USA.
 Vermögen
Vermögen